Can Conway's Game Of Life Teach Us About Innovation?

The Conway Game Of Life, a fascinating cellular automaton, provides valuable insights into engineering innovation, and at polarservicecenter.net, we’re dedicated to providing comprehensive service and support for your Polar devices. Delve into the world of cellular automata, computational irreducibility, and the evolution of technology within this unique system. Explore resources like troubleshooting guides, warranty details, and repair options to optimize your Polar product’s functionality and keep your wearable tech in peak condition.

1. What Is Conway’s Game of Life?

Conway’s Game of Life is a zero-player game where the evolution of a grid of cells is determined by a set of simple rules. These rules dictate cell survival, death, and birth based on the number of neighboring cells. It is a cellular automation game invented by mathematician John Conway.

Expanding on this, the game is played on a two-dimensional grid of cells, each of which can be in one of two states: alive or dead. The game proceeds through discrete time steps, and the state of each cell in the next time step depends on the states of its eight neighbors. The three rules are:

Any live cell with fewer than two live neighbors dies (underpopulation).
Any live cell with two or three live neighbors lives on to the next generation.
Any live cell with more than three live neighbors dies (overpopulation).
Any dead cell with exactly three live neighbors becomes a live cell (reproduction).

These simple rules can lead to complex and emergent behaviors, making the Game of Life a popular subject for studying computational systems and pattern formation.

What Can We Learn about Engineering and Innovation from Half a Century of the Game of Life Cellular Automaton?

2. What Are The Key Components In Conway’s Game of Life?

Key components include still lifes, oscillators, spaceships, and glider guns, which have become fundamental in building more complex structures. Each plays a vital role in making the game so interesting.

To elaborate:

Still Lifes: These are stable patterns that do not change from one generation to the next. A simple example is a block, which is a 2×2 square of live cells.
Oscillators: These are patterns that return to their initial state after a finite number of generations. The simplest oscillator is a blinker, which alternates between two states every two generations.
Spaceships: These are patterns that move across the grid while maintaining their shape. The most famous spaceship is the glider, which moves diagonally across the grid.
Glider Guns: These are complex patterns that emit spaceships (typically gliders) periodically. The most well-known glider gun is the Gosper glider gun, which emits a glider every 30 generations.
Methuselahs: These are initial patterns with long lifespans before stabilizing into simple oscillators or still lifes.

These components form the basic building blocks for more sophisticated constructions and experiments within the Game of Life, showcasing the emergent complexity arising from simple rules.

3. What Makes Conway’s Game of Life Relevant to Metaengineering?

Conway’s Game of Life offers a unique platform for metaengineering by allowing the study of how bit patterns are invented or discovered within a uniform framework. It’s a controlled environment to study innovation.

Here’s why it’s relevant:

Uniform Framework: Everything in the Game of Life is reduced to patterns of bits, making it easier to study innovation as a pure phenomenon without the complexities of real-world materials and constraints.
Longitudinal Data: Over nearly six decades, the Game of Life has accumulated a vast dataset of engineering innovations, providing a rich history to analyze the arc of progress.
Objective Identification: It allows clear identification of objectives and the processes used to achieve them, whether through human effort or automated search.
Computational Equivalence: The Principle of Computational Equivalence suggests infinite richness within the system, making it an ideal sandbox for exploring engineering and technology paths.
Comparison with Adaptive Evolution: It allows comparison between purposeful human engineering and blind adaptive evolution, providing insights into the nature of innovation.

By studying the Game of Life, researchers can gain insights into the processes of invention, discovery, and optimization that are applicable to broader engineering and technological advancements.

4. How Do Still Lifes, Oscillators, And Spaceships Fit Into The Game?

Still lifes remain constant, oscillators repeat patterns, and spaceships move periodically, each playing a fundamental role in the game’s dynamics and the basis for complex structures. Each provides different ways to build on the game.

Here is an expanded view of their roles:

Still Lifes: These stable structures provide a foundation for building more complex patterns. They can act as anchors or components in larger constructions, ensuring that certain parts of the pattern remain unchanged over time. Examples include the block, beehive, and loaf.
Oscillators: These repeating patterns introduce dynamic behavior into the Game of Life. They can be used as clocks or signal generators in more complex circuits. Examples include the blinker, toad, and pulsar.
Spaceships: These moving patterns allow for the transmission of information or energy across the grid. They are crucial for building computational devices and creating complex interactions between different parts of a pattern. The most famous example is the glider, which can be used to transport signals and trigger events.

The interplay between these basic components enables the creation of intricate and functional structures within the Game of Life, demonstrating how simple rules can lead to emergent complexity.

5. What Is A Glider Gun And Why Is It Important?

A glider gun is a pattern that emits gliders periodically, serving as a signal source for more complex constructions, making it a key component in Game of Life “technology”. It demonstrates continuous growth in the game.

Expanding on its importance:

Signal Generation: Glider guns provide a consistent stream of gliders, which can be used as signals to trigger events or transmit information across the grid. This is analogous to a clock signal in electronic circuits.
Construction of Complex Devices: By directing and manipulating the gliders emitted by a glider gun, it is possible to build logic gates, memory cells, and other computational devices within the Game of Life.
Demonstration of Complexity: The existence of glider guns demonstrates that the Game of Life is capable of producing complex, self-sustaining patterns from simple rules. This has implications for understanding how complexity can arise in natural systems.
Computational Universality: Glider guns are essential for building Turing machines and other computationally universal devices within the Game of Life, showing that the game is capable of performing any computation that a computer can.
Advancements in Efficiency: Discovering more efficient glider guns (e.g., those with shorter periods) represents progress in Game of Life technology, leading to more compact and faster constructions.

The glider gun, therefore, is not just a curiosity but a fundamental component that enables advanced engineering and computational possibilities within the Game of Life.

6. How Did The Discovery Of The Glider Gun Impact The Game?

The discovery of the glider gun in 1970 was a significant breakthrough, showing that the Game of Life could support sustained growth and paving the way for more complex engineering feats.

To elaborate on its impact:

Enabled Self-Replication: The glider gun proved that the Game of Life was capable of producing patterns that could sustain themselves indefinitely, countering the initial belief that all patterns would eventually stabilize or die out.
Opened New Avenues for Research: It inspired researchers to look for other complex patterns and mechanisms within the Game of Life, leading to the discovery of spaceships, puffers, breeders, and other interesting structures.
Facilitated Complex Constructions: The glider gun provided a source of gliders that could be used as signals to build logic gates, memory cells, and other computational devices, paving the way for more advanced engineering projects.
Demonstrated Computational Universality: By using glider guns to construct Turing machines and other computationally universal devices, researchers showed that the Game of Life was capable of performing any computation that a computer can.
Inspired Theoretical Insights: The discovery of the glider gun contributed to the understanding of how complex behavior can emerge from simple rules and had implications for fields such as artificial life and complex systems theory.

Overall, the discovery of the glider gun revolutionized the study of the Game of Life and transformed it from a simple pastime into a rich area of scientific exploration.

7. Can You Explain The Concept Of A “Puffer” In The Game Of Life?

A puffer is a spaceship that leaves debris behind as it moves, creating a trail of persistent structures, contrasting with spaceships that leave no trace.

Here’s a more detailed explanation:

Definition: A puffer is a type of spaceship that, as it moves across the grid, leaves a trail of stable or oscillating patterns behind it. These patterns can be still lifes, oscillators, or even other, smaller spaceships.
Contrast with Spaceships: Unlike regular spaceships, which move without altering the environment behind them, puffers continuously modify the grid as they travel. This results in a growing pattern that expands over time.
Mechanism: Puffers typically achieve this behavior by emitting gliders or other small patterns that interact with the environment and create the debris trail. The design of a puffer requires careful coordination of these emissions to ensure that the debris is stable and does not disrupt the puffer’s movement.
Examples: One of the early examples of a puffer is the “block-laying switch engine,” which leaves a trail of blocks behind it.
Significance: Puffers demonstrate another level of complexity within the Game of Life, showing how patterns can not only move but also actively modify their surroundings. They have been used in the construction of complex devices and have contributed to the understanding of pattern formation in cellular automata.

Puffers, therefore, add another dimension to the Game of Life, showcasing how dynamic patterns can interact with and transform their environment.

8. What Is A “Breeder” And How Does It Work In Conway’s Game Of Life?

A breeder uses streams of gliders to create glider guns, which then generate more gliders, leading to exponential growth of glider guns in the game. It’s a complex system.

Here’s an in-depth explanation of how it works:

Definition: A breeder is a complex pattern in the Game of Life that creates glider guns, which in turn produce gliders. This leads to a self-replicating structure where the number of glider guns increases over time.
Mechanism: The original breeder design involves a series of glider collisions that construct glider guns. Gliders from an initial set of glider guns are directed to specific locations where they interact to form new glider guns. These new glider guns then begin emitting their own streams of gliders, continuing the process.
Quadratic Growth: The growth of glider guns in a breeder is typically quadratic, meaning that the number of glider guns increases proportionally to the square of the number of generations. This is because each glider gun produces a constant stream of gliders, and the number of glider guns increases linearly over time.
Complexity: Breeders are among the most complex patterns in the Game of Life, requiring a large number of cells and intricate coordination of glider streams. They demonstrate the game’s capacity for self-replication and exponential growth.
Significance: Breeders are important because they show how complex structures can emerge from simple rules and how self-replication can occur in cellular automata. They have also inspired theoretical work on self-replicating systems and artificial life.

The breeder, therefore, represents a significant milestone in the study of the Game of Life, highlighting its potential for creating complex, self-replicating structures.

9. What Are “Hasslers” and How Do They Contribute to Optimizations?

Hasslers “mine” small pieces of computational irreducibility, “harnessing” behavior by returning patterns to their original states after performing a desired action, contributing to optimizations.

To expand on this:

Definition: Hasslers are small patterns that are designed to interact with specific unstable configurations in the Game of Life, stabilizing them and causing them to oscillate or perform other desired actions.
Mechanism: Hasslers work by carefully exploiting the inherent computational irreducibility of the Game of Life. They are designed to trigger specific reactions in the target configuration, causing it to transform and evolve in a controlled manner. After the desired action has been performed, the hassler returns the configuration to its original state, allowing the process to be repeated.
Mining Computational Irreducibility: By harnessing the computational irreducibility of the Game of Life, hasslers can perform complex operations with relatively simple structures. This allows for the creation of compact and efficient devices.
Optimizations: Hasslers contribute to optimizations by allowing for the creation of smaller, faster, and more robust patterns. They can be used to reduce the size of oscillators, spaceships, and other complex structures, making them more practical for use in larger constructions.
Examples: There are hasslers designed to stabilize various unstable configurations, causing them to oscillate with specific periods or emit gliders at regular intervals.

Hasslers, therefore, are a crucial tool for optimizing patterns in the Game of Life, allowing for the creation of more efficient and compact devices.

10. How Does The Principle Of Computational Equivalence Relate To Game of Life?

The Principle of Computational Equivalence suggests that Game of Life, as a computationally universal system, can perform any computation, emphasizing the balance between simplicity and potential complexity. It shows infinite richness.

Here’s how it connects:

Computational Universality: The Principle of Computational Equivalence states that once a system reaches a certain level of complexity, it is capable of performing any computation that any other system can perform. The Game of Life is known to be computationally universal, meaning that it can simulate any Turing machine or computer algorithm.
Balance Between Simplicity and Complexity: Despite its simple rules, the Game of Life exhibits complex and unpredictable behavior. This is consistent with the Principle of Computational Equivalence, which suggests that even simple systems can give rise to arbitrarily complex computations.
Unpredictability: The Principle of Computational Equivalence implies that it is impossible to predict the long-term behavior of the Game of Life in general. This is because the game is capable of performing computations that are undecidable, meaning that there is no algorithm that can determine their outcome in advance.
Implications for Engineering: The Principle of Computational Equivalence suggests that there are limits to what can be achieved through engineering in the Game of Life. While it is possible to construct complex devices and patterns, there will always be inherent unpredictability and limitations due to the game’s computational universality.
Mining the Computational Universe: The Principle of Computational Equivalence also suggests that there is a vast space of possible computations that can be performed within the Game of Life. This motivates researchers to “mine” the computational universe for patterns that perform useful tasks or exhibit interesting behaviors.

Overall, the Principle of Computational Equivalence provides a theoretical framework for understanding the balance between simplicity and complexity in the Game of Life and its implications for engineering and computation.

11. What Is “Computational Irreducibility” And How Does It Affect The Game?

Computational irreducibility means that some systems can only be understood by running them, making prediction impossible and driving the need for experimentation in Game of Life.

To break it down further:

Definition: Computational irreducibility is a principle stating that some computational processes cannot be shortcut or simplified. In other words, the only way to determine the outcome of such a process is to run it step-by-step.
Impact on Prediction: Computational irreducibility implies that it is impossible to predict the long-term behavior of certain patterns in the Game of Life without actually running the simulation. This is because the game is capable of performing computations that are inherently complex and cannot be reduced to simpler forms.
Emergent Behavior: Computational irreducibility is a key factor in the emergence of complex and unpredictable behavior in the Game of Life. Even though the rules of the game are simple, the interactions between cells can give rise to patterns that are impossible to anticipate.
Engineering Challenges: Computational irreducibility poses challenges for engineering in the Game of Life. It means that it is difficult to design patterns that perform specific tasks with certainty, as their behavior may be sensitive to small changes in initial conditions or interactions with other patterns.
Motivation for Experimentation: Computational irreducibility motivates experimentation and exploration in the Game of Life. Since it is impossible to predict the behavior of patterns in advance, researchers must rely on simulation and observation to discover new phenomena and develop new techniques.

Computational irreducibility, therefore, is a fundamental aspect of the Game of Life that shapes its behavior and poses challenges for its study and engineering.

12. How Do The Concepts of “Construction” and “Search” Differ in Game of Life?

“Construction” involves explicit engineering by humans to build patterns, while “search” uses algorithms to discover new patterns automatically, representing different approaches to innovation. Each method is valuable.

Expanding on their differences:

Construction: This approach involves human designers creating patterns from scratch, using their knowledge of the rules of the Game of Life and existing patterns to build specific structures with desired behaviors. Construction often relies on modular design, where complex patterns are assembled from simpler components.
Search: This approach involves using computer algorithms to automatically explore the space of possible Game of Life patterns, looking for configurations that exhibit interesting behaviors. Search algorithms may use random generation, genetic algorithms, or other techniques to efficiently explore the pattern space.
Explicit vs. Implicit Knowledge: Construction relies on explicit knowledge of the rules of the Game of Life and the behavior of existing patterns, while search relies on implicit knowledge encoded in the search algorithm and the evaluation function used to assess the quality of patterns.
Human Effort vs. Automation: Construction requires significant human effort and ingenuity, while search can be largely automated, allowing computers to explore vast regions of the pattern space.
Complementary Approaches: Construction and search are often used in combination. For example, a designer may use construction to create a framework for a pattern, and then use search to find specific components that fit within that framework.

Both construction and search have contributed to the discovery of new patterns and techniques in the Game of Life, and they represent complementary approaches to innovation in this computational system.

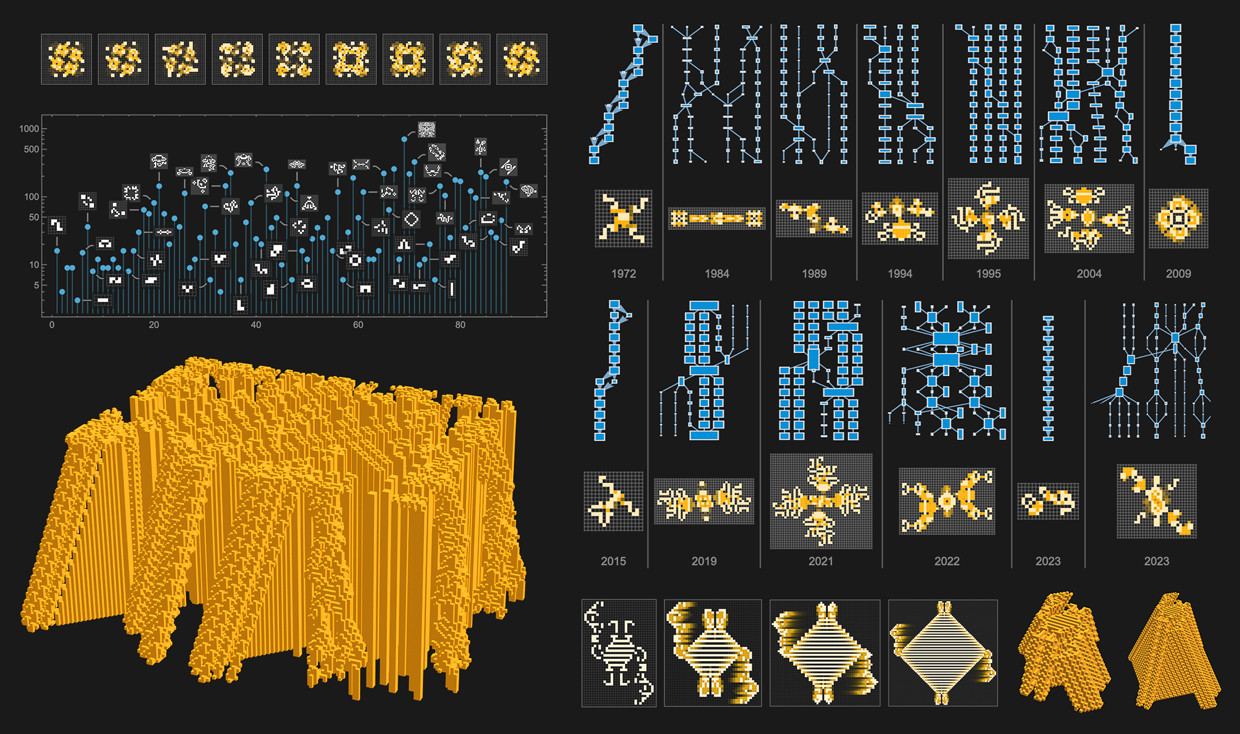
13. What Can We Learn From The “Arc of Progress” In Game of Life?

The “arc of progress” in Game of Life shows waves of activity, influenced by new techniques (like search algorithms) and community collaboration, offering lessons on how innovation evolves. It shows different focuses over time.

Here’s what we can learn:

Phases of Innovation: The arc of progress in the Game of Life is characterized by distinct phases of activity, with periods of rapid innovation followed by periods of relative quiescence. These phases often correspond to the introduction of new techniques or tools, such as search algorithms or online communities.
Cumulative Nature of Innovation: Innovations in the Game of Life build upon previous discoveries, with new patterns often incorporating elements from earlier designs. This cumulative nature of innovation highlights the importance of preserving and sharing knowledge within the community.
Role of Community: The Game of Life community has played a crucial role in the arc of progress, with individuals and groups collaborating to discover new patterns, develop new techniques, and share their findings with others.
Influence of Technology: The availability of faster computers and online communication tools has significantly impacted the pace of innovation in the Game of Life. These technologies have enabled researchers to perform larger-scale searches and collaborate more effectively.
Importance of Objectives: The arc of progress in the Game of Life is shaped by the objectives that researchers set for themselves. The discovery of new patterns and techniques is often driven by a desire to achieve specific goals, such as finding smaller oscillators or more efficient spaceships.

By studying the arc of progress in the Game of Life, we can gain insights into the dynamics of innovation in other complex systems, including technology, science, and society.

14. How Has Modularity Affected The Development In Game of Life?

Modularity, constructing systems from independent subsystems, has been key in Game of Life, allowing complex structures to be built from simpler components, improving design and understanding.

Here’s an in-depth explanation:

Definition: Modularity refers to the degree to which a system is composed of independent, self-contained components that can be combined and reused in different contexts. In the Game of Life, modularity refers to the extent to which patterns can be broken down into smaller, interacting parts that perform specific functions.
Impact on Design: Modularity has greatly influenced the development of the Game of Life by allowing designers to create complex structures from simpler components. By assembling patterns from reusable modules, designers can create more intricate and functional devices than would be possible if they had to design everything from scratch.
Improved Understanding: Modularity also improves our understanding of Game of Life patterns. By breaking down complex patterns into smaller, more manageable parts, we can gain insights into how they work and how they can be modified or improved.
Causal Graphs: Causal graphs are used to represent the modular structure of Game of Life patterns, showing how different parts of the pattern interact and influence each other over time. These graphs can be used to identify independent modules and to understand the flow of information and energy within the pattern.
Optimization: Modularity can also contribute to the optimization of Game of Life patterns. By identifying and replacing inefficient modules with more efficient ones, designers can reduce the size, complexity, and computational cost of their patterns.

Overall, modularity has been a key factor in the development of the Game of Life, enabling the creation of complex, functional, and efficient patterns.

15. Can You Provide Examples Of Modularity In Game Of Life Engineering?

Examples include using basic components like glider guns, reflectors, and conduits to build complex circuits, demonstrating how modular design enables intricate functionality.

Here are some specific examples:

Glider-Based Logic Gates: Gliders can be used to represent signals in the Game of Life, and collisions between gliders can be used to implement logic gates such as AND, OR, and NOT. By combining these logic gates, it is possible to build complex circuits that perform arbitrary computations.
Memory Cells: Gliders can also be used to create memory cells that store information. One common design involves using a glider stream to toggle the state of a flip-flop, which can then be read out by another glider stream.
Multiplexers and Demultiplexers: These devices can be used to route signals between different parts of a circuit. They are typically constructed from combinations of logic gates and glider streams.
Adders and Multipliers: These arithmetic circuits can be built using glider-based logic gates and memory cells. They can perform addition and multiplication on binary numbers represented by glider streams.
Complete Computers: By combining these modular components, it is possible to build complete computers within the Game of Life. These computers are typically slow and inefficient compared to electronic computers, but they demonstrate the computational universality of the Game of Life.

These examples illustrate how modular design can be used to create complex and functional systems in the Game of Life, highlighting the power of this approach to engineering and computation.

16. Why Was There A “Dry Spell” In Finding Spaceships And Guns?

The “dry spell” from the early 1970s to the 1990s occurred because finding these structures often relies on computational irreducibility, requiring extensive search rather than straightforward construction.

Here’s an elaboration:

Computational Irreducibility: The discovery of spaceships and guns often relies on finding specific configurations that exhibit complex and unpredictable behavior. This is due to the computational irreducibility of the Game of Life, which means that it is impossible to predict the long-term behavior of certain patterns without actually running the simulation.
Limited Computational Resources: In the early years of the Game of Life, computational resources were limited, making it difficult to perform the extensive searches required to discover new spaceships and guns. As computers became faster and more powerful, it became easier to explore the pattern space and find these elusive structures.
Shift in Focus: In the early years, there was a greater emphasis on construction, where patterns were designed from scratch using human knowledge and intuition. As search algorithms became more sophisticated, there was a shift towards automated exploration of the pattern space, leading to the discovery of new spaceships and guns.
Community Dynamics: The Game of Life community also played a role in the dry spell. In the early years, there was a smaller community of researchers working on the game, and communication and collaboration were more limited. As the community grew and online communication tools became more prevalent, it became easier to share ideas and coordinate search efforts.

The dry spell in finding spaceships and guns, therefore, was a result of a combination of factors, including computational irreducibility, limited computational resources, a shift in focus from construction to search, and the dynamics of the Game of Life community.

17. What Strategies Are Used To “Tame” Irreducibility For Engineering Purposes?

“Taming” computational irreducibility involves using hasslers and similar techniques to constrain unpredictable behavior, enabling the creation of reliable components for Game of Life systems.

Here’s how it’s done:

Hasslers: These are small, carefully designed patterns that interact with specific unstable configurations, stabilizing them and causing them to oscillate or perform other desired actions. By harnessing the computational irreducibility of the Game of Life, hasslers can perform complex operations with relatively simple structures.
Constraints: Engineers often impose constraints on the patterns they design, limiting the range of possible behaviors and making it easier to predict and control their interactions. For example, they may require patterns to be symmetrical, or to operate within a specific region of the grid.
Feedback Loops: Feedback loops can be used to stabilize patterns and make them more robust to perturbations. By monitoring the state of a pattern and adjusting its behavior accordingly, engineers can create systems that are self-regulating and self-correcting.
Modular Design: Modular design involves breaking down complex systems into smaller, more manageable components that can be designed and tested independently. This makes it easier to understand and control the behavior of the overall system.
Simulation and Testing: Engineers rely on simulation and testing to explore the behavior of their designs and identify potential problems. By running simulations under different conditions, they can identify vulnerabilities and refine their designs to make them more robust.

By using these strategies, engineers can tame the computational irreducibility of the Game of Life and create reliable components for building complex systems.

18. What Are Conduits and Reflectors and What Role Do They Play?

Conduits guide glider streams, while reflectors change their direction, enabling signal routing and manipulation, crucial for building complex circuits and logic gates in the game.

Expanding on their roles:

Conduits: These patterns act as channels or pathways for glider streams, guiding them from one location to another. They are essential for routing signals within a Game of Life circuit and for directing gliders to specific locations to trigger events.
Reflectors: These patterns change the direction of glider streams, allowing engineers to redirect signals and create more complex pathways. Reflectors can be designed to reflect gliders at different angles, depending on the specific requirements of the circuit.
Signal Routing: Conduits and reflectors are used in combination to create complex signal routing networks within the Game of Life. By carefully arranging these components, engineers can direct signals to different parts of the circuit and control the flow of information.
Logic Gates: Conduits and reflectors can also be used to build logic gates, which are the fundamental building blocks of digital circuits. By using glider collisions and other interactions between glider streams, engineers can implement AND, OR, NOT, and other logic functions.
Complex Circuits: By combining conduits, reflectors, and logic gates, it is possible to build complex circuits within the Game of Life. These circuits can perform a wide range of tasks, from simple arithmetic to complex data processing.

Conduits and reflectors, therefore, are essential components for building complex circuits and logic gates in the Game of Life, enabling engineers to create sophisticated computational devices within this simple computational system.

19. Can The Game Of Life Emulate A Turing Machine?

Yes, Game of Life can emulate a Turing machine, showcasing its computational universality, meaning it can perform any computation a computer can, highlighting its theoretical significance.

Here’s an explanation:

Computational Universality: The ability to emulate a Turing machine is a key indicator of computational universality. A system that can emulate a Turing machine is capable of performing any computation that a computer can perform.
Construction of a Turing Machine: In the Game of Life, a Turing machine can be constructed using gliders to represent the tape, states, and head of the machine. Logic gates and memory cells are used to implement the transition rules of the Turing machine.
Challenges: Emulating a Turing machine in the Game of Life is a complex and challenging task, requiring a large number of cells and intricate coordination of glider streams. However, several successful implementations have been demonstrated.
Theoretical Significance: The ability to emulate a Turing machine in the Game of Life has significant theoretical implications. It demonstrates that the Game of Life is capable of performing any computation that can be performed by a computer, highlighting its potential for exploring the foundations of computation and information processing.
Practical Applications: While emulating a Turing machine in the Game of Life is not practical for real-world computation, it has inspired the development of new techniques for building complex systems in other domains, such as artificial intelligence and robotics.

The fact that the Game of Life can emulate a Turing machine underscores its importance as a model for understanding computation and complexity.

20. What Are The Implications of Discovering “Objects With Unusual Growth”?

Discovering “objects with unusual growth” reveals the potential for unexpected behaviors and computational irreducibility, suggesting unexplored possibilities within the Game of Life.

Here’s why it’s important:

Unpredictable Behavior: Objects with unusual growth exhibit patterns that are difficult to predict or categorize. They may grow in unexpected ways, change their shape over time, or interact with other patterns in complex and surprising ways.
Computational Irreducibility: The behavior of objects with unusual growth is often computationally irreducible, meaning that it is impossible to predict their long-term behavior without actually running the simulation. This highlights the inherent complexity and unpredictability of the Game of Life.
New Possibilities: Objects with unusual growth may represent new possibilities for engineering and computation in the Game of Life. They may be used as building blocks for new types of devices, or they may inspire new techniques for harnessing the computational power of the Game of Life.
Scientific Insights: Studying objects with unusual growth can provide insights into the fundamental principles of computation, information processing, and self-organization. They may help us to better understand how complex systems can emerge from simple rules.
Further Exploration: The discovery of objects with unusual growth motivates further exploration of the Game of Life and other cellular automata. By studying these patterns and their interactions, we may uncover new phenomena and develop new techniques for harnessing their computational power.

The discovery of objects with unusual growth, therefore, is an important reminder of the vast and unexplored potential of the Game of Life.

21. How Do “Hasslers” Relate To Harnessing Computational Irreducibility?

Hasslers exploit computational irreducibility to control specific behaviors, using the game’s complexity to create simple, repeatable actions, balancing chaos and order.

Here’s an explanation:

Harnessing Complexity: Hasslers are designed to interact with specific unstable configurations in the Game of Life, harnessing their inherent computational irreducibility to perform complex operations.
Controlled Behavior: By carefully designing the hassler pattern, engineers can cause the target configuration to transform and evolve in a controlled manner. This allows them to perform specific actions, such as oscillating with a desired period or emitting gliders at regular intervals.
Stabilization: Hasslers often stabilize unstable configurations, preventing them from collapsing or evolving into unpredictable patterns. This is achieved by carefully balancing the interactions between the hassler and the target configuration.
Repeatable Actions: After the desired action has been performed, the hassler returns the configuration to its original state, allowing the process to be repeated. This ensures that the hassler can be used to perform the same action multiple times without disrupting the overall system.
Balance: Hasslers represent a balance between chaos and order, harnessing the computational irreducibility of the Game of Life while maintaining control over the behavior of the system. They are a powerful tool for creating compact and efficient devices in the Game of Life.

By using hasslers, engineers can harness the complexity of the Game of Life and create simple, repeatable actions, demonstrating the power of this approach to taming computational irreducibility.

22. How Does The Idea Of “Lifetime Hacking” Apply To Game of Life?

“Lifetime hacking” involves finding or creating patterns that survive as long as possible, pushing the limits of the game and demonstrating the potential for complex, sustained behavior.

Here’s how it works:

Maximizing Survival: The goal of lifetime hacking is to find or create patterns that survive for as long as possible before dying out. This can be achieved by carefully designing the initial configuration of cells to maximize the likelihood of survival.
Computational Limits: Lifetime hacking pushes the limits of the Game of Life, challenging researchers to find patterns that exhibit complex and sustained behavior. This can lead to new insights into the fundamental principles of computation, information processing, and self-organization.
Complex Behavior: Patterns that survive for long periods of time often exhibit complex and unpredictable behavior. They may change their shape over time, interact with other patterns in surprising ways, or give rise to new and unexpected phenomena.
Exploration: Lifetime hacking encourages exploration of the Game of Life and other cellular automata. By experimenting with different initial conditions and patterns, researchers can uncover new possibilities and develop new techniques for maximizing survival.
Engineering Challenge: Lifetime hacking can also be viewed as an engineering challenge. By carefully designing patterns to maximize their survival time, engineers can create systems that are more robust, resilient, and adaptable.

Lifetime hacking, therefore, is a fascinating area of exploration within the Game of Life, pushing the boundaries of what is possible and demonstrating the potential for complex, sustained behavior in this simple computational system.

23. How Does Adaptive Evolution Compare To Purposeful Engineering In Game Of Life?

Adaptive evolution, a “blind” process, often results in “lumps of irreducible computation,” while purposeful engineering seeks understandable, modular designs, reflecting different approaches to problem-solving.

Here are the key differences:

Adaptive Evolution: This approach involves starting with a random configuration of cells and then making small, random changes to the pattern over time. The goal is to find patterns that exhibit desired behaviors, such as long survival times or the ability to perform specific tasks.
Purposeful Engineering: This approach involves human designers creating patterns from scratch, using their knowledge of the rules of the Game of Life and existing patterns to build specific structures with desired behaviors.
Irreducible Computation: Adaptive evolution often results in patterns that are difficult to understand or analyze. These patterns may be composed of “lumps of irreducible computation,” meaning that their behavior cannot be simplified or predicted without actually running the simulation.
Understandable Designs: Purposeful engineering, on the other hand, seeks to create patterns that are understandable and predictable. These patterns are often composed of modular components that interact in well-defined ways.
Efficiency: Adaptive evolution can be very efficient at finding patterns that achieve specific goals, but it may not result in patterns that are easy to understand or modify. Purposeful engineering, on the other hand, may result in patterns that are less efficient but more understandable and easier to maintain.

Adaptive evolution and purposeful engineering, therefore, represent two different approaches to problem-solving in the Game of Life, each with its own strengths and weaknesses.

24. What Questions Arise When Trying To Determine If A Pattern Was “Made For A Purpose”?

Determining if a pattern was “made for a purpose” raises questions about intention, conciseness, and whether the pattern’s behavior aligns with a recognized objective within the Game of Life.

Here are the key questions:

Intention: Was the pattern deliberately designed to achieve a specific goal, or did it arise randomly through chance or evolution?
Conciseness: Is the pattern the most concise way to achieve its goal, or is there a simpler or more efficient solution?
Alignment: Does the pattern’s behavior align with a recognized objective within the Game of Life, such as oscillating with a specific period, emitting gliders, or surviving for a long time?
Purpose: Is the purpose well-defined, and does the pattern directly achieve it without unnecessary complexity?
Construction: Does the pattern consist of modular parts or show signs of explicit design that suggests purposeful intention?

By addressing these questions, researchers can gain insights into the origins and intentions behind Game of Life patterns and better understand the relationship between design, purpose, and complexity in this computational system.

25. How Can Causal Graphs Help Determine If A Pattern Was Invented Or Discovered?

Causal graphs can reveal the modularity of a pattern; constructed patterns often have distinct, interacting components, while discovered patterns may appear as irreducible “blobs,” indicating different origins.

Here’s how causal

Can Conway’s Game Of Life Teach Us About Innovation?